情報の単位と計算
10進数と2進数
155は2進数で
128・64・32・16・8・4・2・1
10011011・・128+0+ 0+16+8+0+2+1=155 〇
10110011・・128+0+32+16+0+0+2+1=179 ✖
11001101・・128+64+・・・・・ ✖
ーーーーーーーーー
01011010+01101011=(2進数で)
ア00110001 ィ01111011 ゥ10000100 ㋓11000101
最も簡単なのは、10進数の足し算のように2進数同士の和を筆算で求める方法です。日常使っている10進数では10で一つ上の桁に繰り上がるように、2進数では2で繰り上がります(1+1=10)。

別の方法としては、2進数を一度10進数に変換し、それを加算した後に再び2進数に戻すこともできます。
- 1. 2つの2進数をそれぞれ10進数に変換する
- 010110102=26+24+23+21
=64+16+8+2=9010
011010112=26+25+23+21+20
=64+32+8+2+1=10710 - 2. 10進数同士を加算する
- 90+107=197
- 3. 2.の結果を2進数に戻す
- 19710=128+64+4+1
=27+26+22+20=110001012
どちらの方法でも答えは11000101になります。したがって「エ」が正解です。
ーーーーーーー
2進数1.101を10進数で表現したものはどれか。
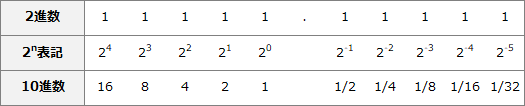
2進数1.101は、(1+0.1+0.001)(2)なので、各桁を10進数に変換したものを足し合わせることで10進数に変換します。
1.101(2)
=(1+1/2+1/8)(10)
=(1+0.5+0.125)(10)
=1.625(10)
したがって、2進数1.101は10進数で1.625となります。
ーーーーーーー
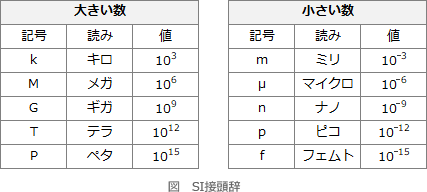
10のマイナス3乗はn、10の3乗はG